梯度下降法(Gradient Descent)是一个广泛被用来最小化模型误差的参数优化算法,它未必是最优的计算权重参数的方法,但是作为一种简单快速的方法,常常被使用。
对于训练得到的模型,如:
$$ h(x) = {w_1x_1 + w_2x_2 … + w_nx_n + b } = {W^TX+b} $$
我们会定义一个loss function来评估该模型的好坏,如:
$$ J(W) = {\sum_{i}^n (h(x^{(i)}) - y^{(i)})^2 \over2} $$
优化的目标就是使得J(W)达到最小值。
梯度下降法流程如下:
|
|
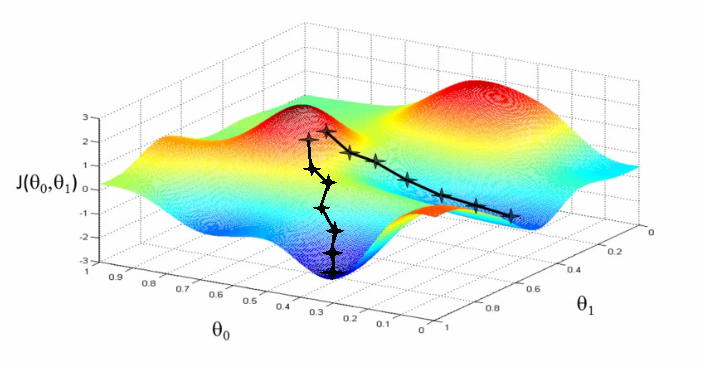
如上图所示,每次梯度变化如下:
$$ W_i = {W_i - \epsilon \frac{\partial J(W)}{\partial W}} = {W_i - \epsilon(h(x)-y)x^{(i)}} $$
用更简单的数学语言描述:
$$ W = {W - \epsilon \nabla J} = {W - \epsilon \nabla
\left| \begin{array}{ccc}\frac{\partial J}{\partial W_0}\
… \
\frac{\partial J}{\partial W_n}\end{array} \right|} $$
其中 ε 为学习率(learning rate),是一个确定步长大小的正标量。
另外,梯度是有方向的,对于一个向量W,每一维分量$W_i$都可以求出一个梯度的方向,我们就可以找到一个整体的方向,在变化的时候,我们就朝着下降最多的方向进行变化就可以达到一个最小点。
当存在多个局部最小值点或平坦区域时,优化算法可能无法收敛到全局最小点。但在深度学习的背景下,即使找到的解不是真正最小的,但只要它们对应于代价函数显著低的值,我们通常就能接受这样的解。
常用的梯度下降法还具体包含有三种不同的形式,它们也各自有着不同的优缺点:
- 批量梯度下降法BGD
批量梯度下降法(Batch Gradient Descent)是梯度下降法最原始的形式,它的具
体思路是在更新每一参数时都使用所有的样本来进行更新,它得到的是一个全局最优解,但是每迭代一步,都要用到训练集所有的数据。
优点:全局最优解,迭代的次数相对较少。
缺点:当样本数目很多时,训练过程会很慢。 - 随机梯度下降法SGD
随机梯度下降法(Stochastic Gradient Descent)通过每个样本来迭代更新一次,如果样本量很大的情况(例如十几万),那么可能只用其中几万条或者几千条的样本,就已经迭代到最优解了,对比上面BDG迭代一次需要用到十几万训练样本,一次迭代不可能最优,如果迭代10次的话就需要遍历训练样本10次。但是,SGD伴随的一个问题是噪音较BGD要多,使得SGD并不是每次迭代都向着整体最优化方向。这种每次只使用单个样本的优化算法有时被称为在(on-line)算法。
优点:训练速度快。
缺点:准确度下降,并不一定收敛到全局最优。 - 小批量梯度下降法MBGD
小批量梯度下降法(Mini-batch Gradient Descent)在上面两张方式中取了一个折衷,在每次更新参数时使用batch_size个样本,即保证了算法的训练过程比较快,也保证最终参数训练的准确率。
大部分深度学习算法都是基于小批量梯度下降法算法求解的,现在通常将它们简单地称为随机梯度下降法方法。
随机梯度下降的核心是:梯度是期望,期望可使用小规模的样本近似估计。具体而言,在算法的每一步,我们从训练集中均匀抽出一小批量(minibatch)样本m′,大小从一到几百。重要的是,当训练集大小m增长时,m′通常是固定的。我们可能在拟合几十亿的样本时,每次更新计算只用到几百个样本。
学习率
为了能够使得梯度下降法有较好的性能,我们需要把学习率的值设定在合适的范围内。学习率决定了参数移动到最优值的速度快慢。如果学习率过大,很可能会越过最优值,出现超调现象,即在极值点两端不断发散,或是剧烈震荡,总之随着迭代次数增大loss没有减小的趋势;反而如果学习率过小,优化的效率可能过低,长时间算法无法收敛,无法快速地找到好的下降的方向,随着迭代次数增大loss基本不变,所以学习率对于算法性能的表现至关重要。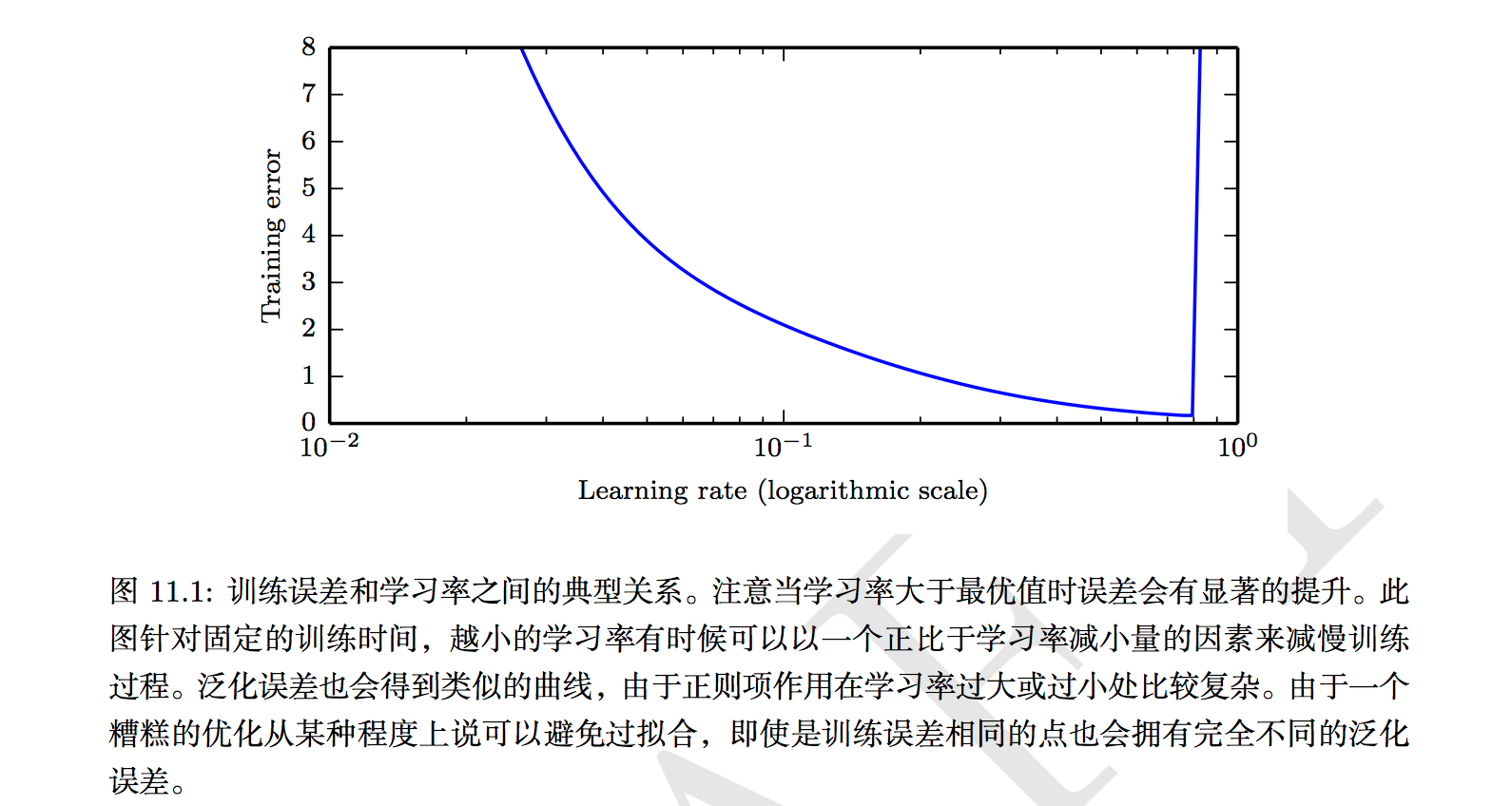
常用的学习率调整有以下两种方式:
- 基于经验的手动调整。 通过尝试不同的固定学习率,如0.1, 0.01, 0.001等,观察迭代次数和loss的变化关系,找到loss下降最快关系对应的学习率。
- 自适应学习率算法。如:AdaGrad、RMSProp、Adam等。
目前,最流行并且使用很高的优化算法包括 SGD、具动量的 SGD、RMSProp、 具动量的 RMSProp、AdaDelta 和 Adam。
动量
虽然随机梯度下降仍然是非常受欢迎的优化方法,但其学习过程有时会很慢。动量方法旨在加速学习,特别是处理高曲率、小但一致的梯度,或是带噪声的梯度。动量算法积累了之前梯度指数级衰减的移动平均,并且继续沿该方向移动。动量的效果如下图所示: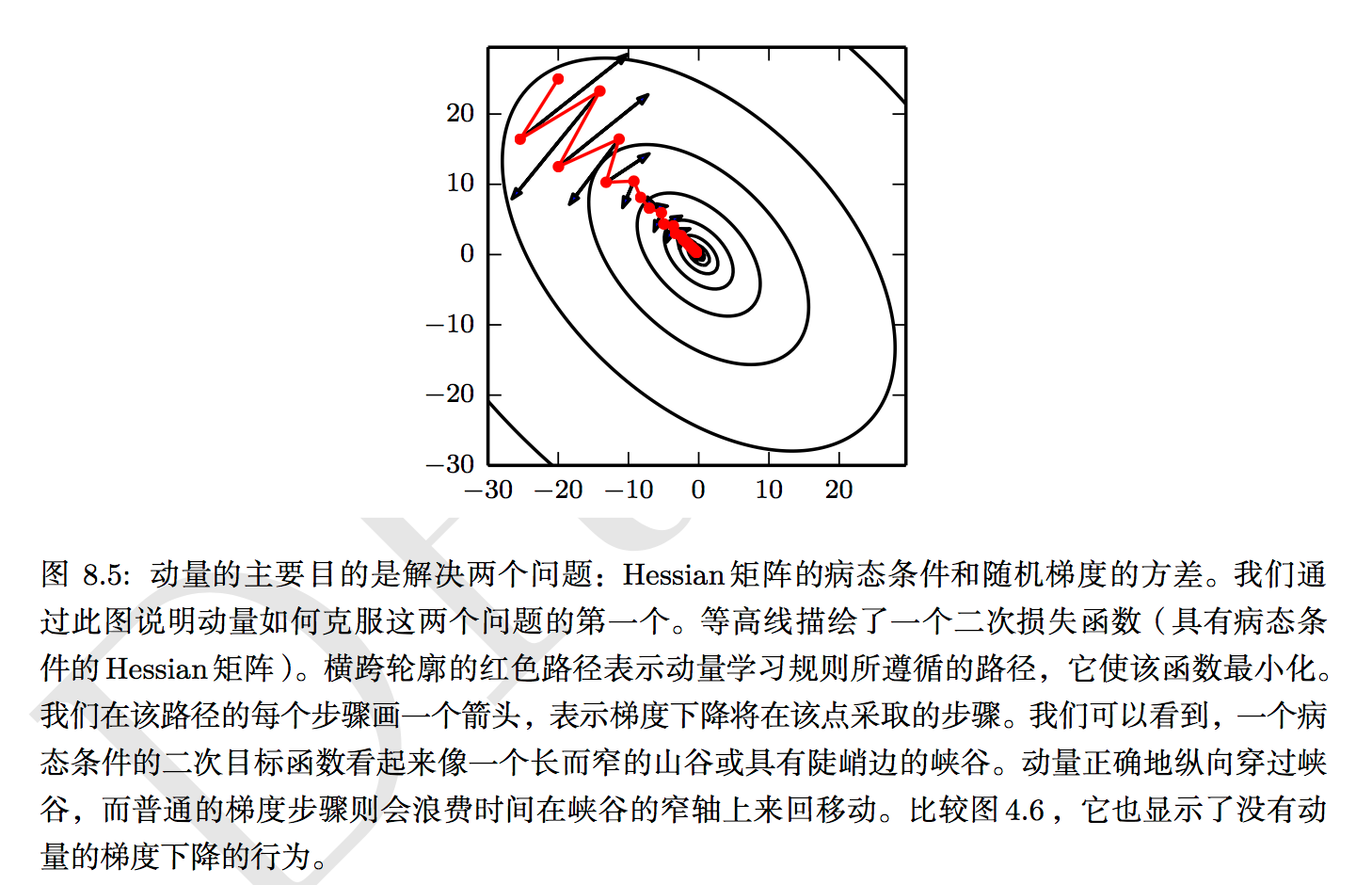
如果动量算法总是观测到梯度g,那么它会在方向 −g 上不停加速,直到达到最终速度,其中步长大小为:
$$ {\epsilon{||g||}\over(1-\alpha)} $$
例如,${\alpha = 0.9}$对应着最大速度10倍于梯度下降算法。在实践中,${\alpha}$的一般取值为0.5、0.9和0.99。和学习率一样,${\alpha}$也会随着时间不断调整。一般初始值是一个较小的值,随后会慢慢变大。随着时间推移调整没${\alpha}$有收缩${\epsilon}$重要。
Batch_Size
在合理范围内,增大Batch_Size 有何好处:
1、内存利用率提高了,矩阵乘法的并行化效率提高。
2、跑完一次epoch(全数据集)所需的迭代次数减少,对于相同数据量的处理速度进一步加快。
3、在一定范围内,一般来说Batch_Size越大,其确定的下降方向越准,引起训练震荡越小。
盲目增大 Batch_Size 有何坏处:
1、内存利用率提高了,但是内存容量可能撑不住了。
2、跑完一次epoch(全数据集)所需的迭代次数减少,要想达到相同的精度,其所花费的时间大大增加了,从而对参数的修正也就显得更加缓慢。
3、Batch_Size增大到一定程度,其确定的下降方向已经基本不再变化。
如上所述,当Batch_Size增大到某个值时,算法可以在时间和最终收敛精度上达到最优。
