CNN手写体识别示例及分析

发表于 | 阅读次数

这里将详细分析深度学习领域一个里程碑之作-CNN(卷积神经网络)，并以上篇文章的手写体识别来做示例。

卷积神经网络

卷积神经网络是一种专门用来处理具有类似网格结构的数据的 神经网络，如图像数据，注意之前的全连接层在训练时只是将图像转换为向量，而忽略了像素在水平和垂直维度上的空间信息，卷积层的作用就是通过使用一个更结构化的权重W来克服这一缺点。
比较好的示例图如下：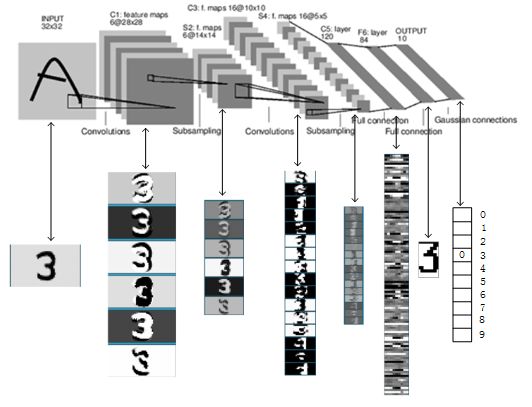


这是一个最典型的卷积网络，由卷积层、池化层、全连接层组成。其中卷积层与池化层配合，组成多个卷积组，逐层提取特征，最终通过若干个全连接层完成分类。
卷积层完成的操作，可以认为是受局部感受野概念的启发，而池化层，主要是为了降低数据维度。
综合起来说，CNN通过卷积来模拟特征区分，并且通过卷积的权值共享及池化，来降低网络参数的数量级，最后通过传统神经网络完成分类等任务。

卷积

一个图像卷积的操作如下：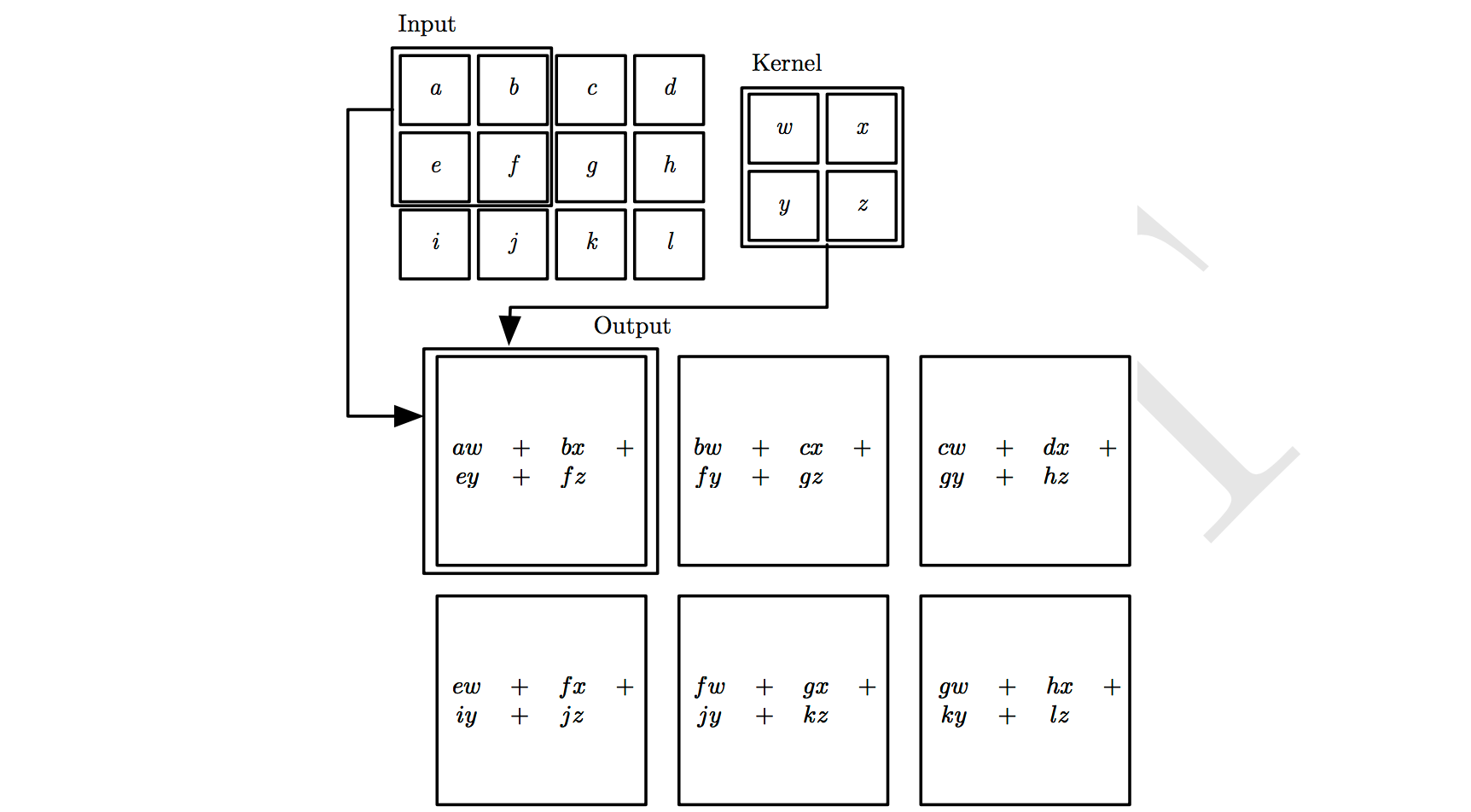

对输入图像应用一个卷积核过滤后得到的结果被成为特征图谱(Feature Map, FM)。假设我们有100种卷积核，没种卷积核学习到的参数都不一样，则它可以提取出输入图像的不同特征，如不同的边缘。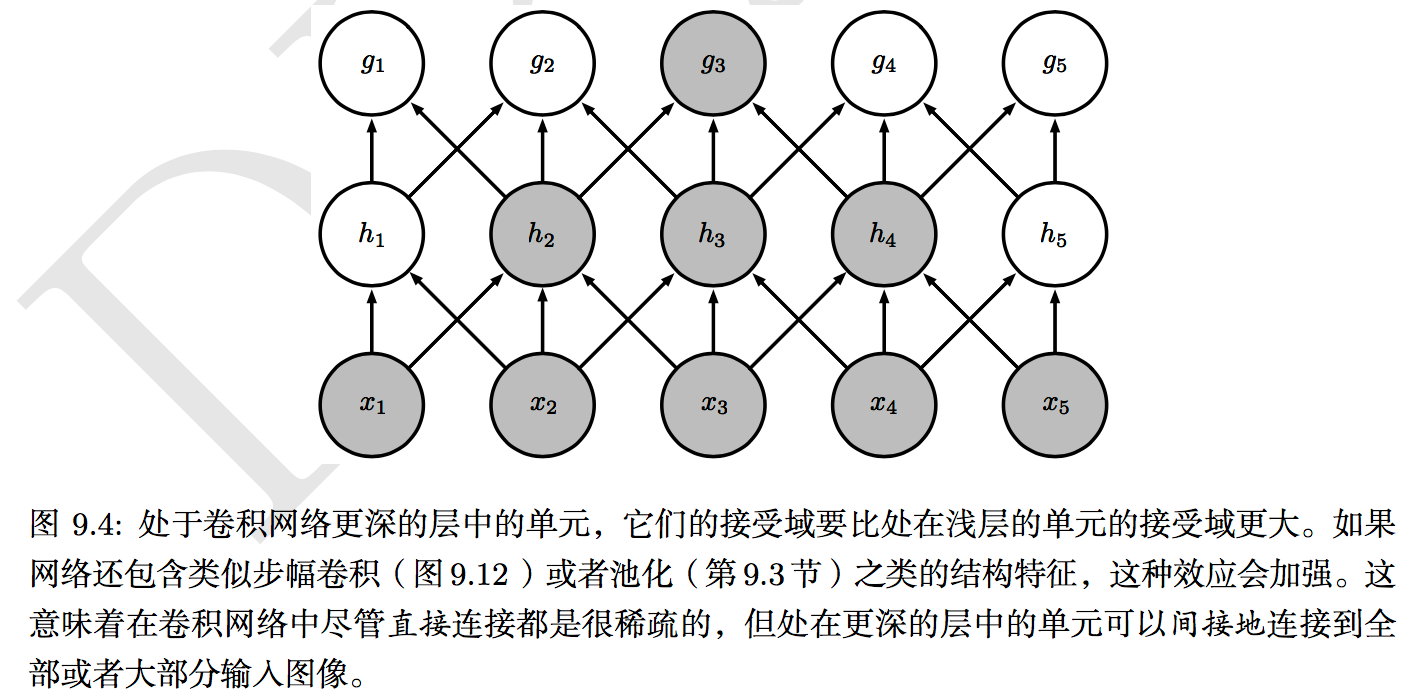

权值共享

直观描述：当从一个大尺寸图像中随机选取一小块如8*8作为样本，并从这个样本中学习到一些特征，那么我们就可以把这个学习到的特征作为探测器，也就是我们的卷积核。我们利用8*8的样本特征跟原本的大尺寸图像做卷积，从而可以在这个大尺寸图中任意一个位置获取一个不同的激活值。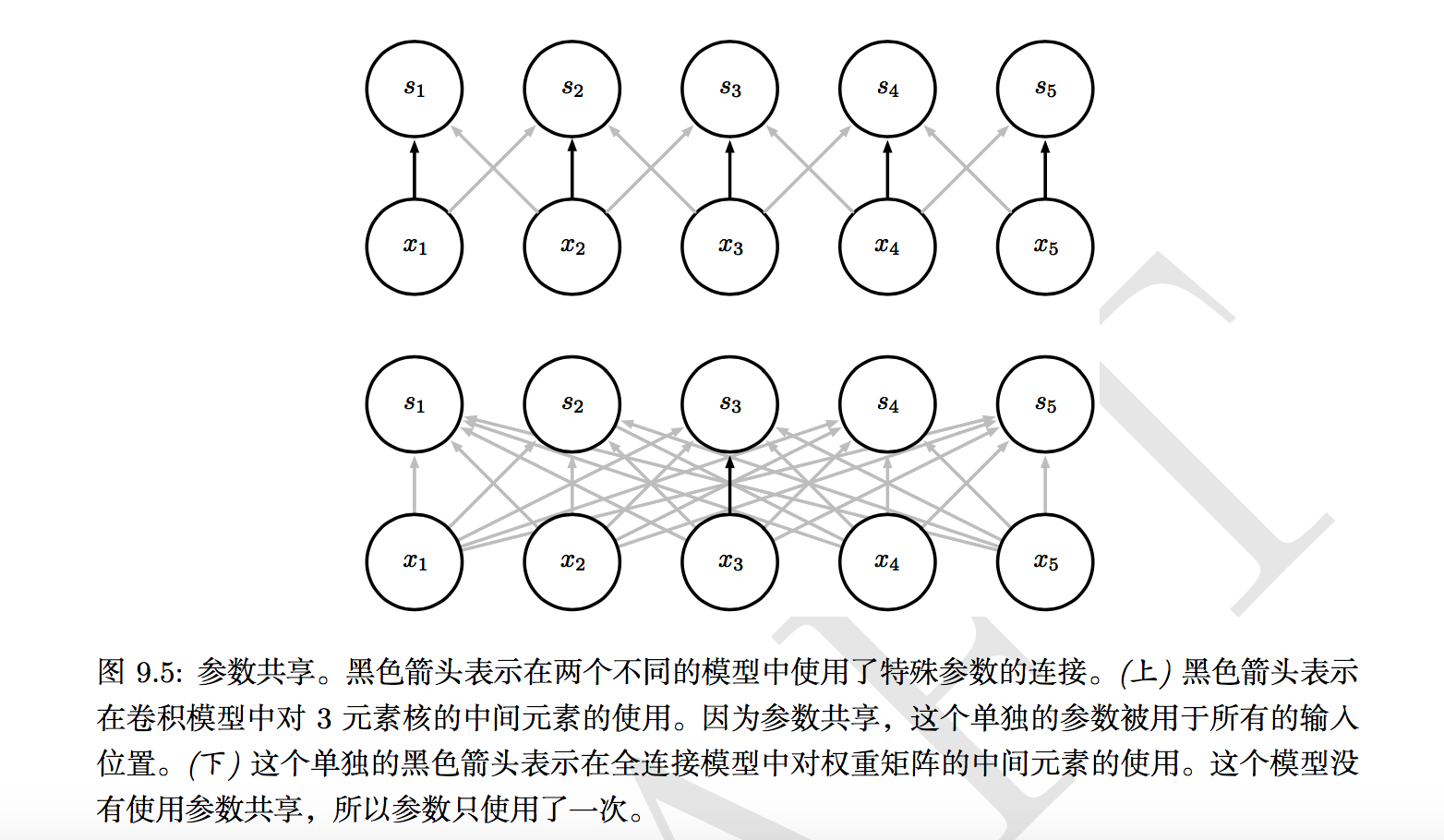

池化

池化函数使用某一位置的相邻输出的总体统计特征来代替网络在该位置的输出。例如，最大池化(max pooling)函数给出相邻矩形区域内的最大值。其他常用的池化函数包括相邻矩形区域内的平均值、L2范数以及基于据中心像素距离的加权平均函数。
使用池化可以看作是增加了一个无限强的先验：这一层学得的函数必须具有对少量平移的不变性。当这个假设成立时，池化可以极大地提高网络的统计效率。
对空间区域进行池化产生了平移不变性，但当我们对分离参数的卷积的输出进行池化时，特征能够学得应该对于哪种变换具有不变性。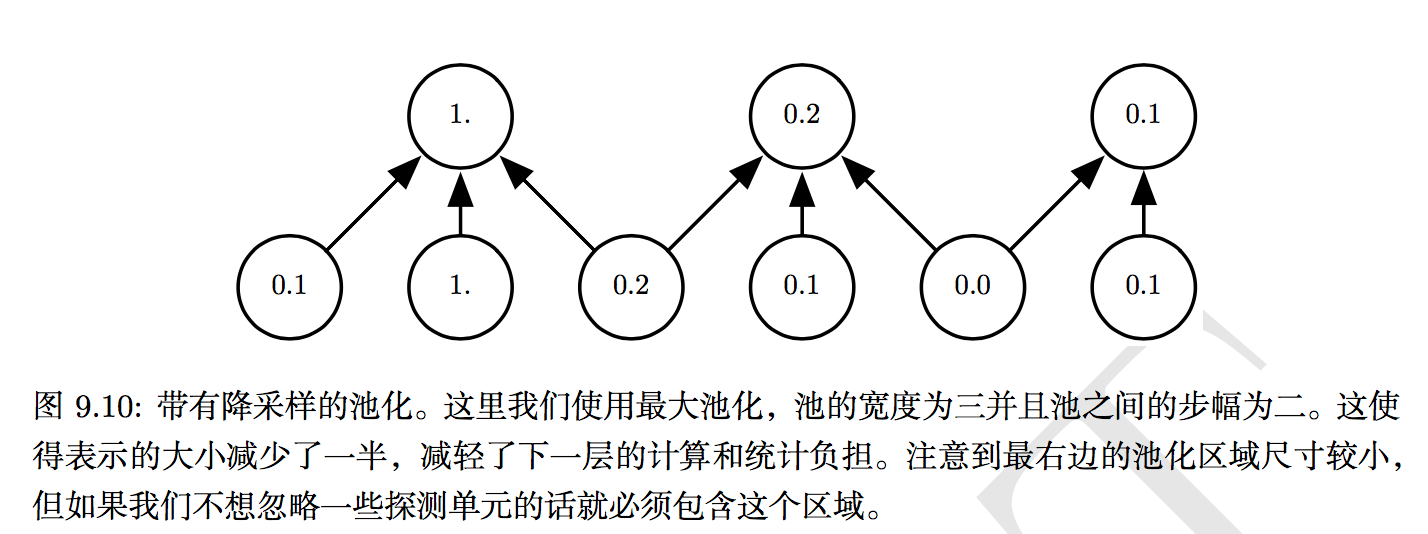

卷积网络相对一般神经网络在图像处理上有如下优点：

  • 输入图像和网络的拓扑结构能更好的吻合；
  • 可以更好用于识别位移、缩放及其他形式扭曲不变性的二维图形；
  • 特征提取和模式分类同时进行，并同时在训练中产生；
  • 权值共享可以减少网络的训练参数，使网络结构变得更简单，适应性更强。

CNN手写体识别示例分析

网络结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#a simple multilayer perceptron
def get_symbol(num_classes=10, **kwargs):
    data= mx.symbol.Variable('data')
    # first conv layer
    conv1= mx.sym.Convolution(data=data, kernel=(5,5), num_filter=20)
    tanh1= mx.sym.Activation(data=conv1, act_type="tanh")
    pool1= mx.sym.Pooling(data=tanh1, pool_type="max", kernel=(2,2), stride=(2,2))
    # second conv layer
    conv2= mx.sym.Convolution(data=pool1, kernel=(5,5), num_filter=50)
    tanh2= mx.sym.Activation(data=conv2, act_type="tanh")
    pool2= mx.sym.Pooling(data=tanh2, pool_type="max", kernel=(2,2), stride=(2,2))
    # first fullc layer
    flatten= mx.sym.Flatten(data=pool2)
    fc1= mx.symbol.FullyConnected(data=flatten, num_hidden=500)
    tanh3= mx.sym.Activation(data=fc1, act_type="tanh")
    # second fullc
    fc2= mx.sym.FullyConnected(data=tanh3, num_hidden=10)
    # softmax loss
    lenet= mx.sym.SoftmaxOutput(data=fc2, name='softmax')   
    shape = {"data":(64, 1, 28, 28)}
    mx.viz.plot_network(symbol=lenet, shape=shape).view()
    return lenet

网络结构如下：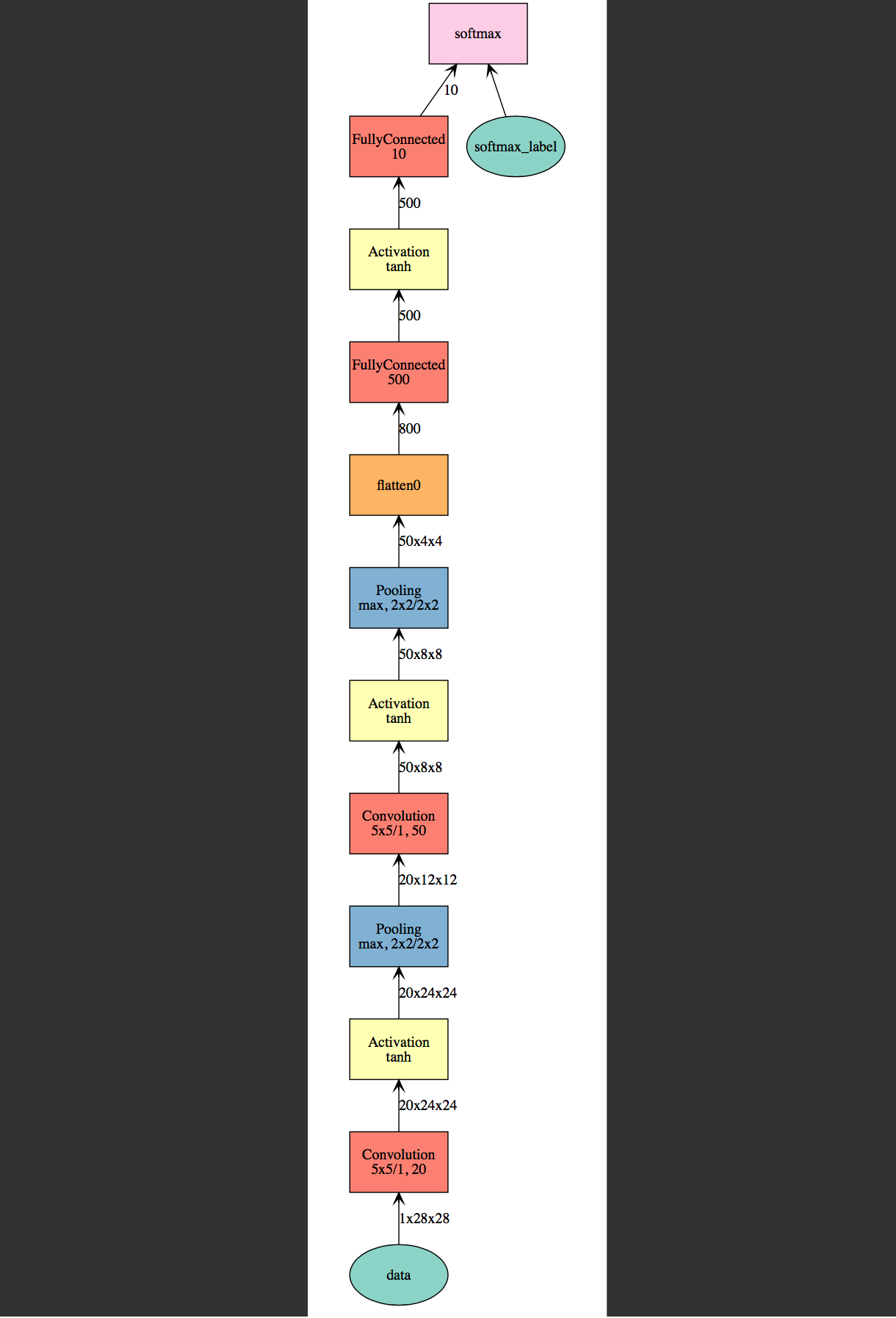

各层维度大小如下：

输入大小 —— 28*28.
第一层卷积 —— 卷积核大小5*5，卷积核个数20，大(28-5+1)*(28-5+1)*20.
第一层池化 —— 池化核大小2*2，步幅大小2*2，大小(24/2)*(24/2)*20.
第二层卷积 —— 积核大小5*5，卷积核个数50，大小(12-5+1)*(12-5+1)*50.
第二层池化 —— 池化核大小2*2，步幅大小2*2，大小(8/2)*(8/2)*50.
flatten层 —— 多维转成一维，维度800.
全连接层 —— 维度500.
全连接层 —— 维度10.
softmax输出 —— 输出为10，输出的每一维都是图片属于该类别的概率

结果输出

1
2
3
4
5
6
7
8
9
10
11
12
13
INFO:root:Epoch[5] Batch [100]	Speed: 1248.19 samples/sec	accuracy=0.998453
INFO:root:Epoch[5] Batch [200]	Speed: 1275.77 samples/sec	accuracy=0.997344
INFO:root:Epoch[5] Batch [300]	Speed: 1292.01 samples/sec	accuracy=0.997812
INFO:root:Epoch[5] Batch [400]	Speed: 1296.30 samples/sec	accuracy=0.999219
INFO:root:Epoch[5] Batch [500]	Speed: 1315.72 samples/sec	accuracy=0.999219
INFO:root:Epoch[5] Batch [600]	Speed: 1270.90 samples/sec	accuracy=0.999375
INFO:root:Epoch[5] Batch [700]	Speed: 1307.15 samples/sec	accuracy=0.999375
INFO:root:Epoch[5] Batch [800]	Speed: 1269.13 samples/sec	accuracy=0.998594
INFO:root:Epoch[5] Batch [900]	Speed: 1328.86 samples/sec	accuracy=0.999531
INFO:root:Epoch[5] Train-accuracy=1.000000
INFO:root:Epoch[5] Time cost=46.563
INFO:root:Saved checkpoint to "./model/mnist-0006.params"
INFO:root:Epoch[5] Validation-accuracy=0.991043

我们看到CNN网络5个epoch训练相对MLP网络的10个epoch的Validation就有明显的提升。
通过feature.py输出个层特征的维度如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
convolution0_output: (10000, 20, 24, 24)
pooling0_output: (10000, 20, 12, 12)
convolution1_output: (10000, 50, 8, 8)
pooling1_output: (10000, 50, 4, 4)
flatten0_output: (10000, 800)
fullyconnected0_output: (10000, 500)
fullyconnected1_output: (10000, 10)
softmax_output: (10000, 10)
如第一个数据最终输出: 
[  4.41006653e-09   1.36926553e-10   1.42115458e-10   6.06908923e-09
   8.65458489e-14   3.72108941e-11   1.22517418e-15   1.00000000e+00
   8.42783092e-13   3.90079524e-09]
它的预测结果如下：
max_output: 1.000000  predict_label: 7  ori_abel: 7 result: True
如果觉得我的文章对您有用，请随意赞赏