人脸检测之SDM

算法介绍

人脸对齐就是在已经检测到的人脸的基础上，自动找到人脸上的眼睛鼻子嘴和脸轮廓等标志性特征位置，通过这一手段可以衍生出很多产品应用，包括美图软件、魔漫相机、表情检测和性别检测等。目前有很多的人脸对齐算法，比较传统的有ASM、AAM、CLM和一些列改进算法，而目前比较流行的有ESR、3D-ESR、SPR、LBF、SDM、CFSS等。这里将详细介绍分析SDM算法，具体参考论文Supervised Descent Method and its Applications to Face Alignment 。
SDM人脸对齐算法属于回归方法，基于回归的方法的基本原理：对于一张给定的人脸，给出一个初始的形状，通过不断地迭代，将初始形状回归到接近甚至等于真实形状的位置。
事实上SDM并非是一种人脸对齐方法，而是一种监督下降方法，用于解决非线性最小化问题。

解决非线性最优化问题通常有2个难点：

（1）方程不可微，计算量太大；
（2）Hessian矩阵太大，不是正定矩阵。

基于这样的难点，作者提出了自己的SDM方法，可以用于解决上述的问题，并成功解决了人脸对齐中关键点的回归问题，具体示意图如下：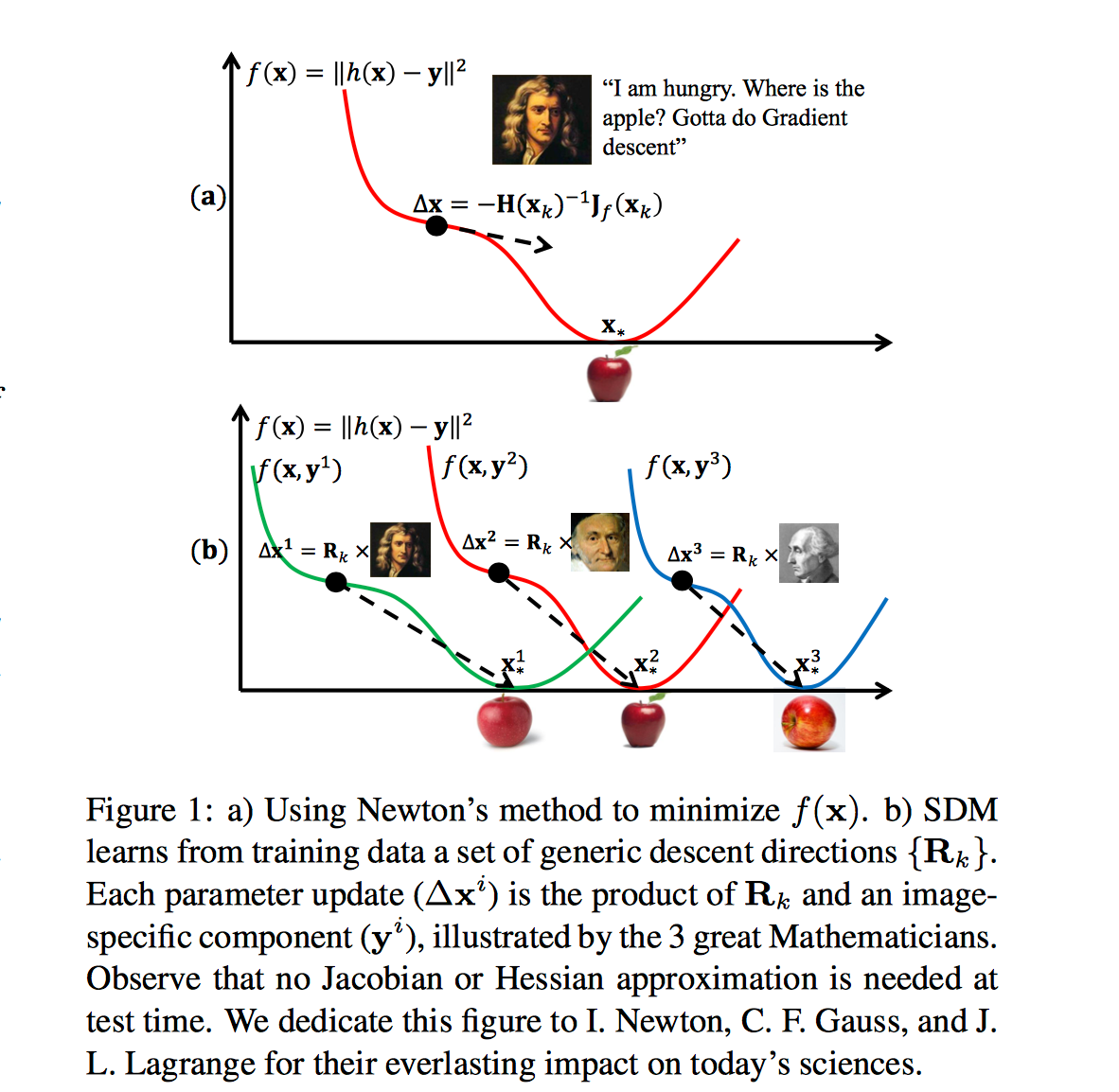

如上图a所示，传统解决最小化二乘问题的方法就是牛顿下山法，通过牛顿迭代，最终可以找到一个全局最小值。这样的迭代也肯定是效果最好的，但是在实际工程应用中，是不会有足够的计算资源来将所有样本一下都计算进去的，于是就有了上图b的方法，更新每一个Δx，每次都会找到一个最小值，然后不断迭代，减少最小值之间的误差距离，最终就会找到全局最小值，类似深度学习里的Mini batch SGD。
给定一张含有m个像素的图片，h表示一个非线性特征提取函数。那么我们的目标就是，在给定一个初始形状x0的基础上，通过回归的方法，将x0回归到该人脸正确的形状x∗上，用数学的方式表达，即为求得使下面的f(x0+Δx)最小的Δx：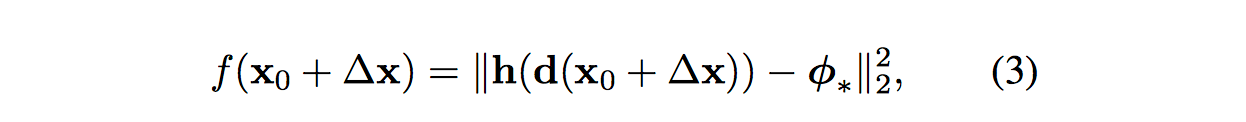

那么问题来了，如果每一张脸的初始形状都是一样的（即都是已知样本的真实形状的平均形状），那么怎么让它们回归到各自人脸的真实形状呢，答案就是每张图片提取出的不同的SIFT特征（具体采用什么特征可以依据情况而定，论文中采用了SIFT特征，但也可以采用如HOG，DOG，甚至LBF等特征）了，虽然采用了相同的初始形状，但在不同的图片上，相同的初始形状所提取出的SIFT特征是完全不同的，也就是ϕ0是不同的，这样就可以通过回归器将其回归到各自的真实形状上了。
现在我们的优化目标，就是要得到一个回归器，这个回归器能起到的作用是将一个初始形状回归到真实形状上去。也就是学到正确的回归器使其得到最好的Δx 。当然想要从初始形状一步步回归到真实形状，只学习一个Δx一般是不行的，因为一步就回归到最小点一般来说要求比较高，即使是牛顿步回归的比较快，通常也不能一步就达到目标。所以我们要学习得到多个不同的回归器，它们依次回归下来，能得到一系列的Δx，这样我们就能很快根据xk+1=xk+Δx得到使目标函数最小的点。
我们使用的是从初始特征点周围提取的SIFT特征作为第一次回归的输入，然而SIFT算子是不可导的，所以如果想要使用一阶或者二阶方法来最小化上面的目标函数，那就只能用数值逼近的方法来估计Jacobian和Hessian矩阵（比如有限差分方法等）。然而数值估计计算量非常大，所以我们要采用SDM方法来学习下降的方向和下降的尺度，或者说学习Jaobian和Hessian矩阵。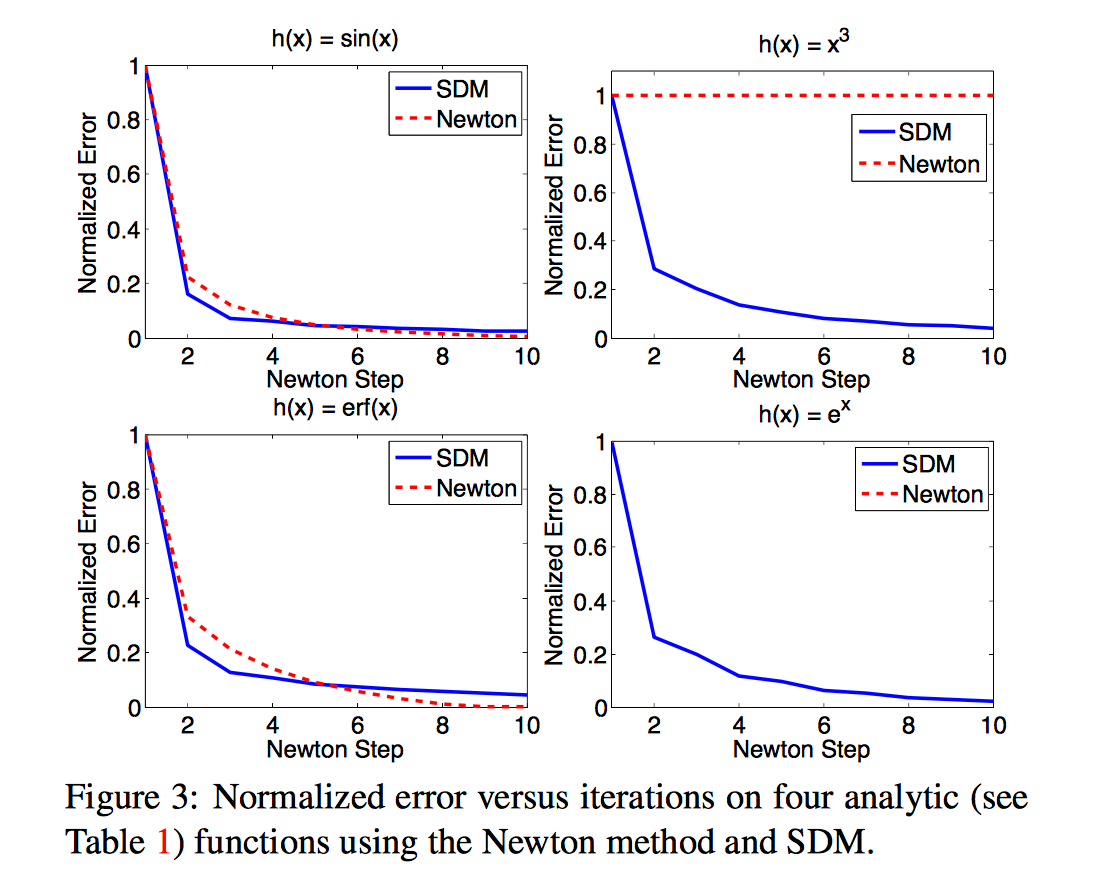

由上图可知SDM的收敛速度比牛顿步更快，只是收敛得最终结果并没有达到最优（比牛顿步差一点），但SDM更具鲁棒性，在函数的Hessian矩阵不是正定的时候，SDM也能很快收敛。