L-Softmax
Softmax Loss函数经常在卷积神经网络中被广泛应用,但是这种形式并不能够有效地学习得到使得类内较为紧凑、类间较离散的特征。论文Large-Margin Softmax Loss for Convolutional Neural Networks提出了L-Softmax loss,能够有效地引导网络学习使得类内距离较小、类间距离较大的特征。
对于Softmax loss而言: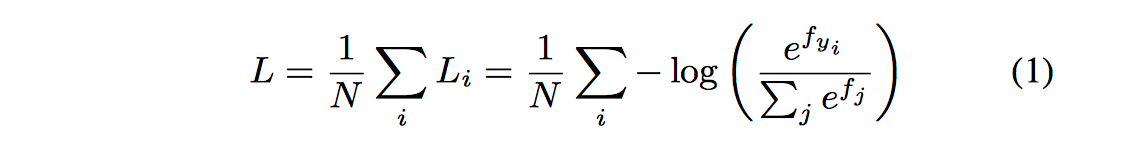
其中fj表示最终全连接层的类别输出向量f的第j个元素,N为训练样本的个数。由于f=W*X是全连接层的激活函数的输出,W和X均为多维向量,最终的损失函数又可以写为: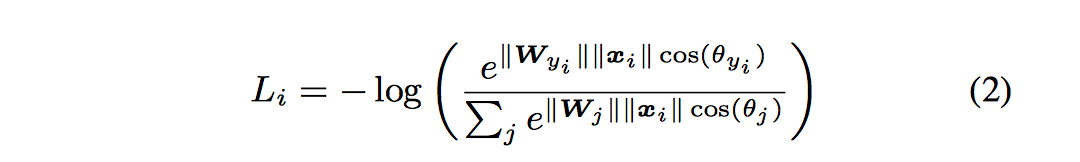
假设一个2分类问题,如果属于类别1的概率大于类别2的概率,则:
L-Softmax loss的动机是希望通过增加一个正整数变量m,从而产生一个决策余量,能够更加严格地约束上述不等式,即:
其中m是正整数,cos函数在0到π范围又是单调递减的,所以cos(mx)要小于cos(x)。m值越大则学习的难度也越大,使得模型可以学到类间距离更大的,类内距离更小的特征,具体示意如下:
最终L-Softmax loss定义如下: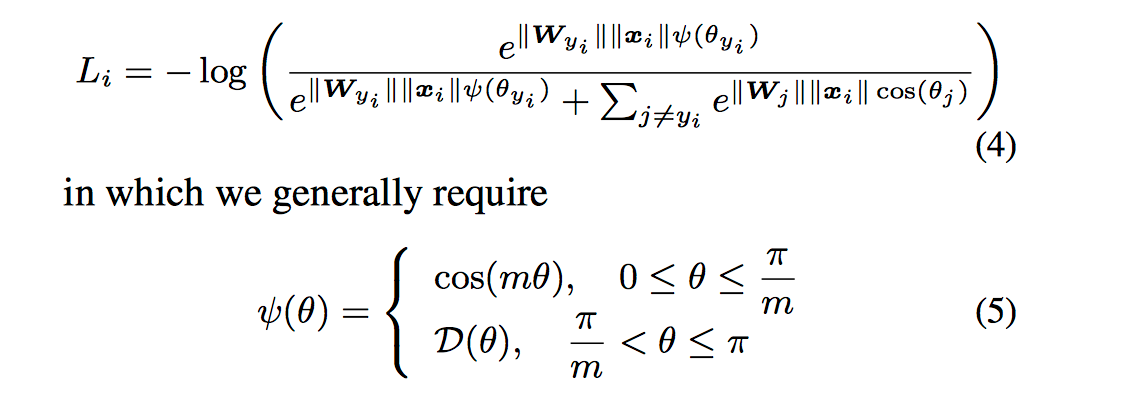
以一个二分类问题为例,L-Softmax loss学习到的参数可以将两类样本的类间距离加大,最后学到的特征之间的分离程度比原来的要明显得多,具体示意图如下: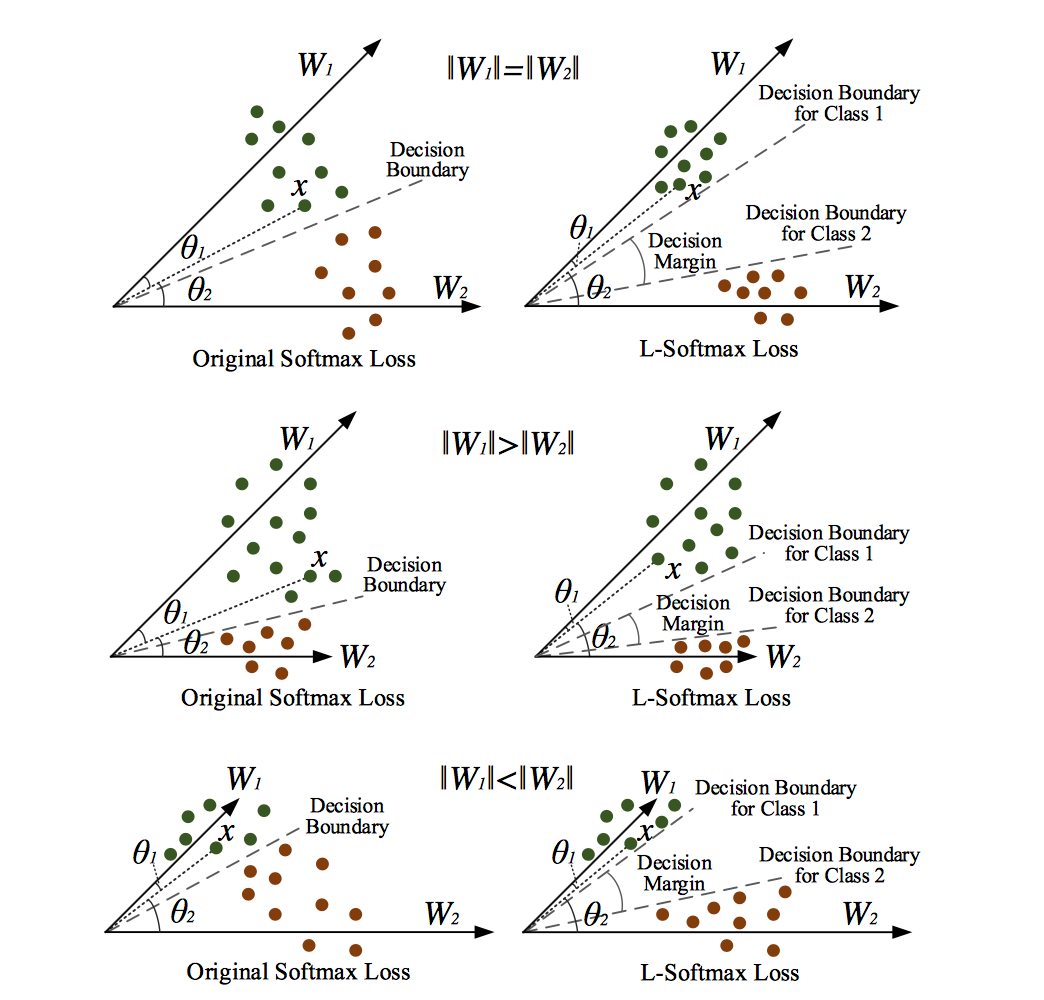
论文在MNIST,CIFAR10以及CIFAR100三个分类问题和人脸比对LFW数据集进行评测,最后的结果是相对于softmax loss,L-Softmax Loss均取得了更好的效果,而且当m越大时,最终的结果会越好。而且论文仅使用了WebFace的人脸数据作为训练集和一个较小的卷积网络,就在LFW上达到了98.71%的正确率,具体LFW测试结果如下:
L-Softmax Loss有一个清楚的几何解释,并且能够通过设置m来调节训练难度。它还能够有效地防止过拟合,能够有效地减小类内距离,同时增加类间距离。最终的分类和人脸验证实验也证明,它确实取得了比softmax loss更好的结果。
A-Softmax
A-Softmax loss是CVPR2017的论文SphereFace: Deep Hypersphere Embedding for Face Recognition提出的,简单来说就是在L-Softmax loss的基础上添加了两个限制条件||W||=1和b=0,使得预测仅取决于W和x之间的角度,具体示意图如下(其中Modified Softmax Loss仅是在Softmax上加入||W||=1和b=0这两个限制条件):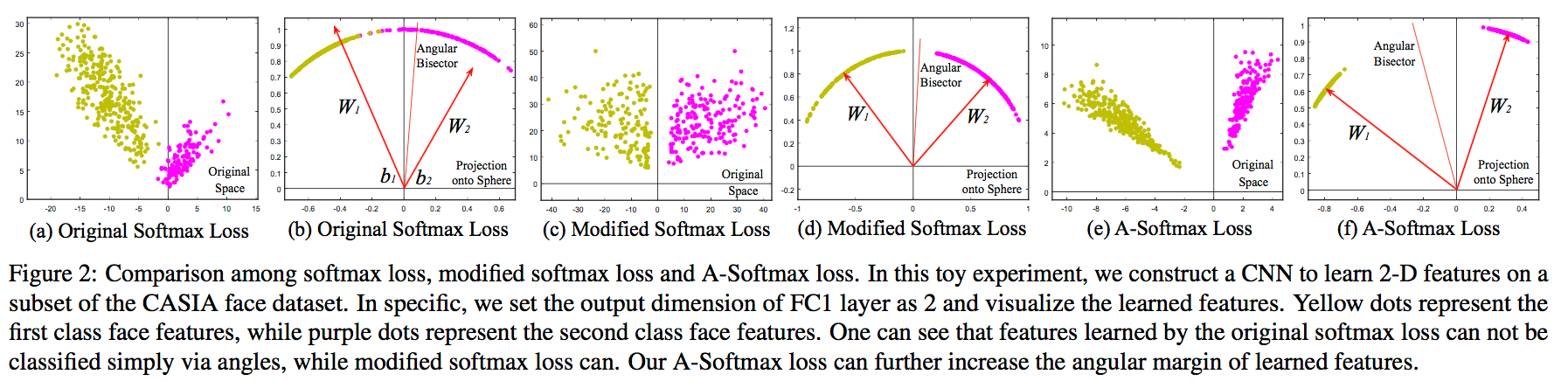
其中Modified Softmax loss数学表达式如下: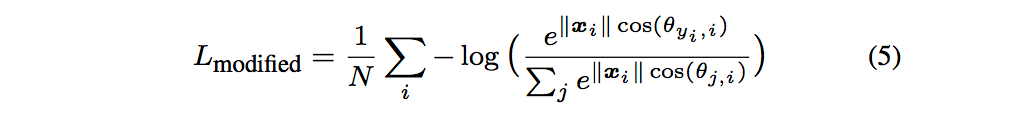
A-Softmax表达式如下: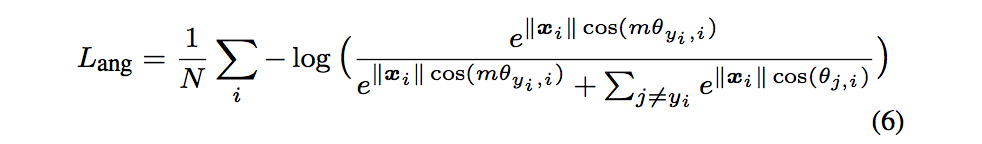
对于一个二分问题,从几何角度看A-Softmax与其他loss的区别: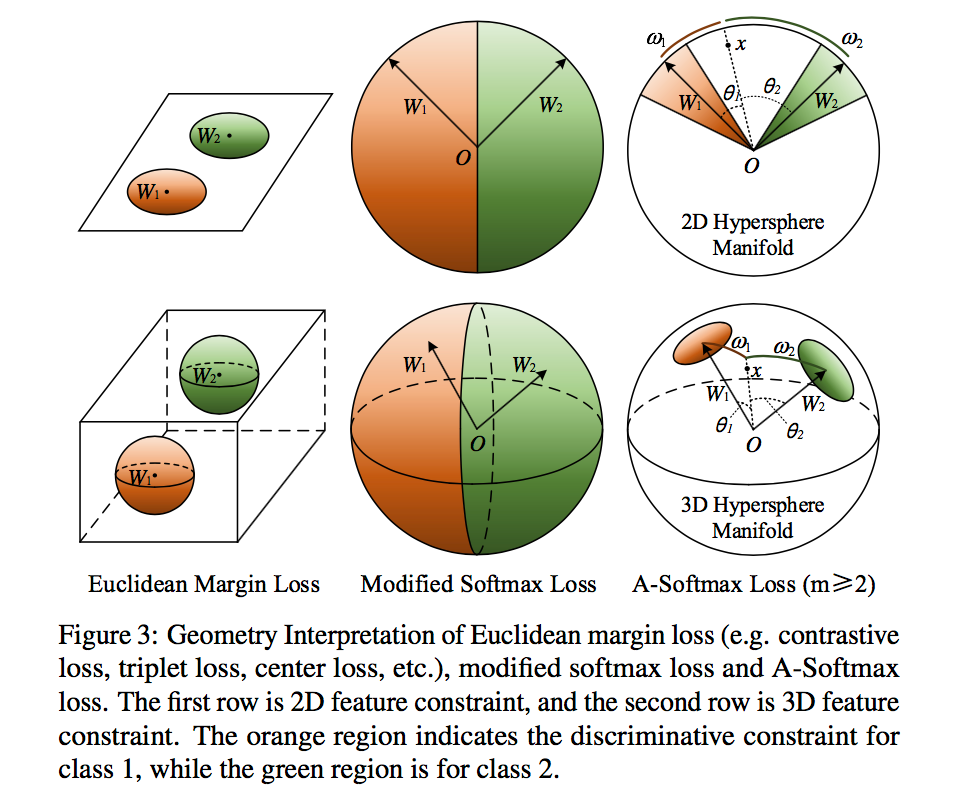
A-Softmax loss在使用时需要注意的一些特性如下:
- 通常情况下,m值越大,学习到的特征区分性更强,但学习难度更大,通常m取4时可以取得较好的效果:
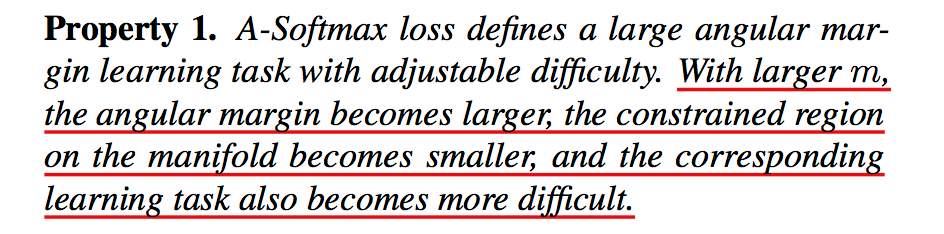
- 针对二分类问题,m最小值值需满足:
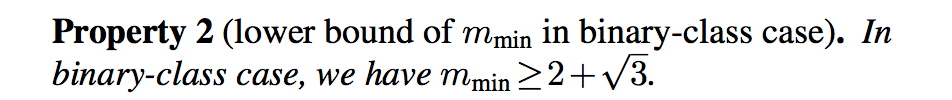
- 针对多分类问题,m最小值需满足:
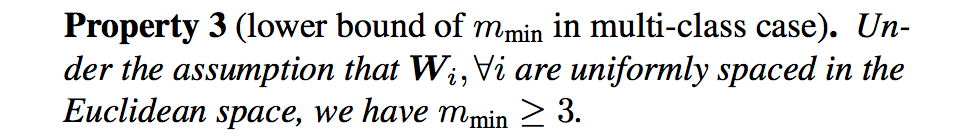
在LFW和YFT上不同m值的表现如下: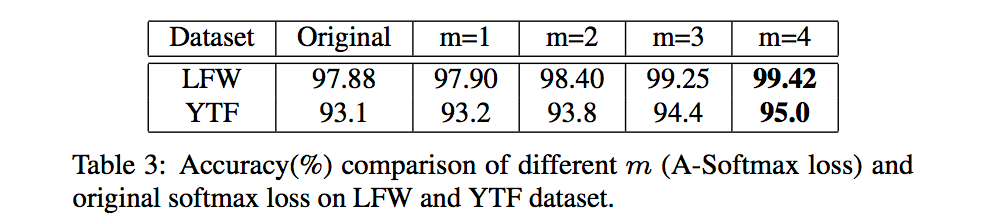
与softmax loss对比如下: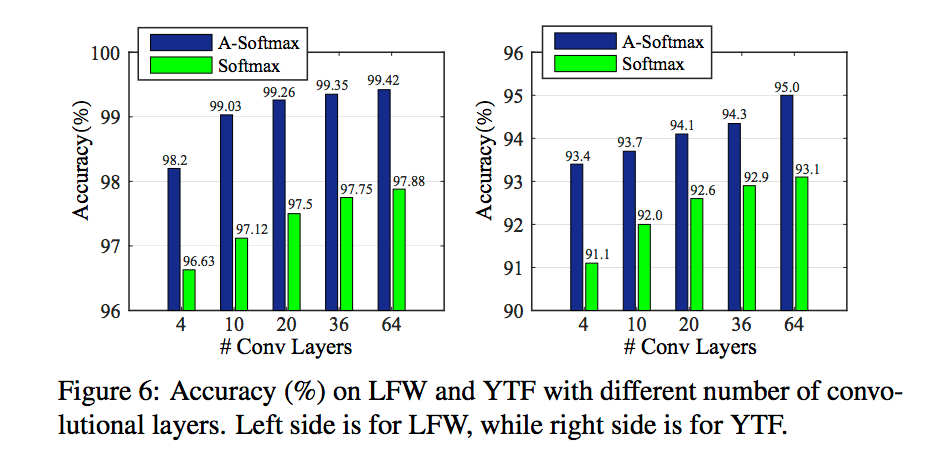
与其他算法对比如下: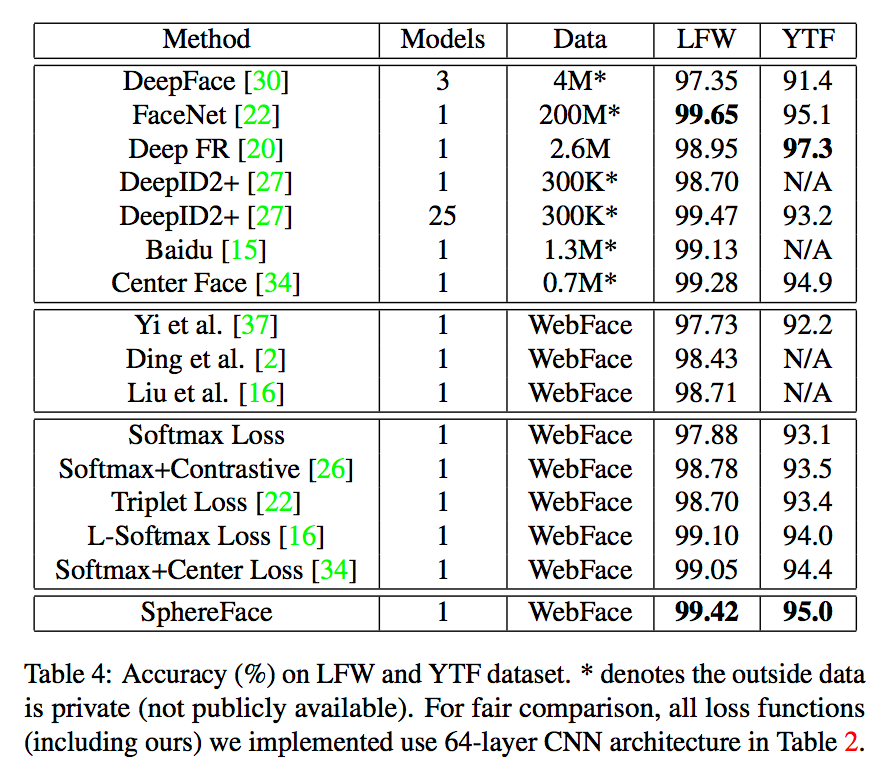
在Megaface上的表现如下: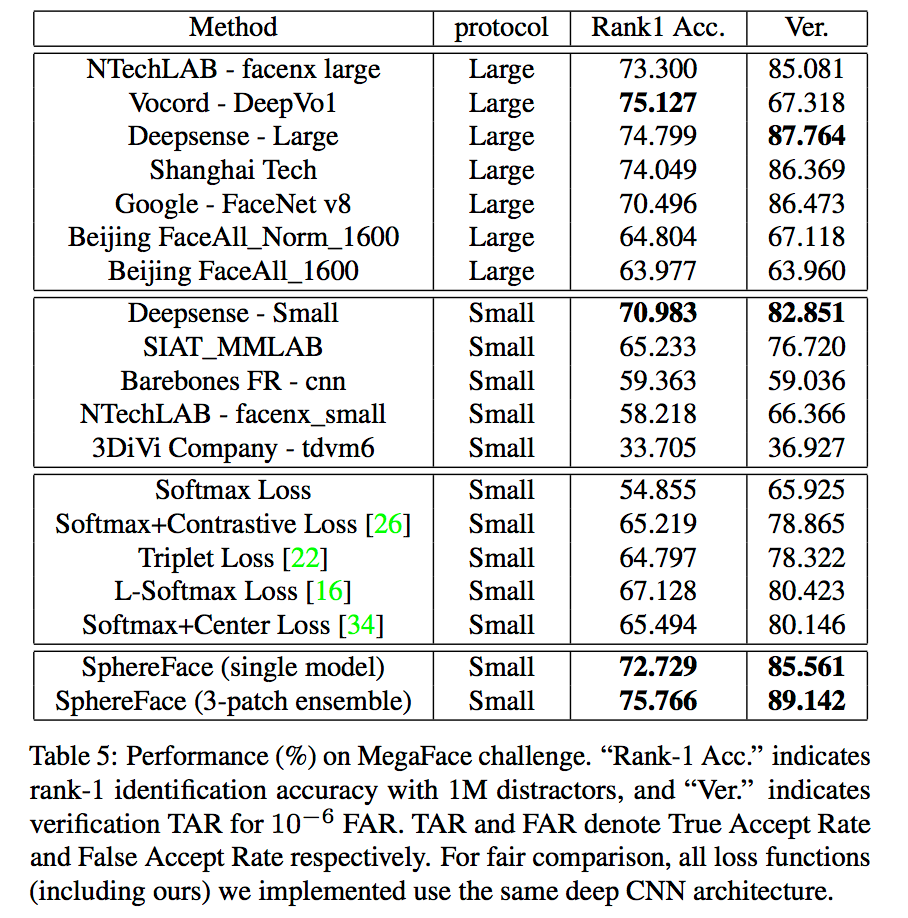
从实验结果可以看出,A-Softmax loss相对L-Softmax和centerloss在效果上会有所提升。
